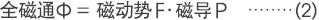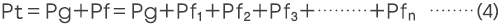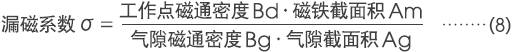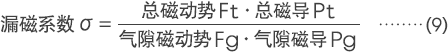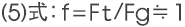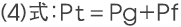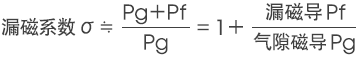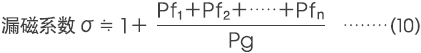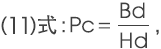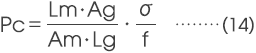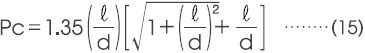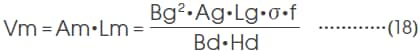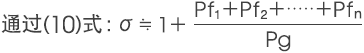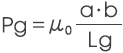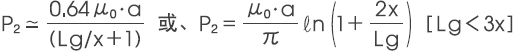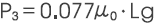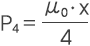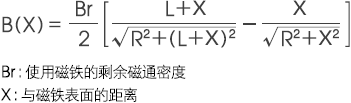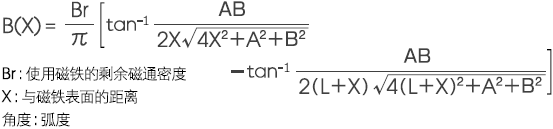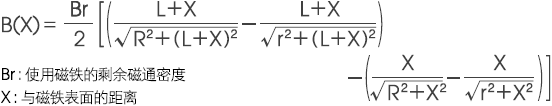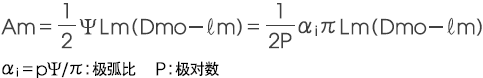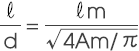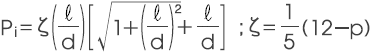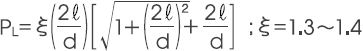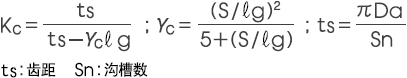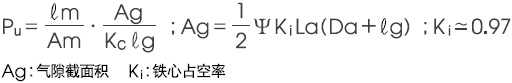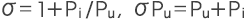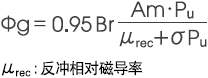磁回路设计资料
1. 基本计算公式
1-1. 全磁通Φ与磁导P
磁回路的基本计算公式与相关的欧姆定律相同。也就是全磁通为Φ,磁动势为F,磁阻为R,该三要素存在如下的关系。
磁路长度为L,磁路截面积为A,磁路的磁导率为μ时,该磁导P采用如下所示的计算公式表示。
依据该计算公式,当磁路长度L变短、磁路截面积A及磁导率μ越大,则磁导P越大(即磁阻变小)。
另外,磁力回路整体的磁导Pt采用气隙部位的磁阻倒数所定义的气隙磁导Pg,与漏磁通所致的磁阻倒数所定义的漏磁导Pf之和来进行表示(Pt=Pg+Pf)。
而且,在掌握各自磁路空间中的漏磁通时,总磁导Pt则用气隙磁导Pg和各自磁路空间中的漏磁导(Pf1+Pf2+Pf3……+Pfn)的总和来进行表示。
1-2. 磁动势损失系数 f
磁动势损失系数f采用磁力回路中的总磁动势Ft与气隙磁动势Fg之比进行定义。
磁力回路中的总磁动势Ft取决于所使用的磁铁特性,其值为磁铁工作点的磁场强度Hd与磁铁长度Lm之乘积。
除此之外,气隙的磁动势Fg取决于气隙磁通密度Bg与气隙长度Lg之乘积,可展开如下面(5)式所示:
1-3. 漏磁系数σ
漏磁系数σ采用磁力回路中的磁铁所产生的总磁通Φt和集中在气隙部位的气隙磁通Φg之比来表示。
磁铁所产生的总磁通Φt,通过磁铁工作点的磁通密度Bd与磁铁截面积Am之积予以赋予,因集中在气隙部位的磁通Φg是通过气隙磁通密度Bg和气隙截面积Ag的积予以确定,故(7)式可以展开如下。
另外,依据公式(2):ø=FP,(7)式同样可采用公式(9)
来进行表示,磁动势损失系数f,一般情况下近似于1,通过将
可采用这种形式进行表示。
1-4. 磁导系数Pc
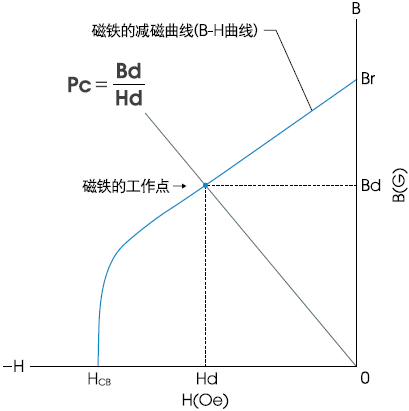
采用磁导系数Pc来表示B-H曲线上的磁铁工作点。该值运用工作点的磁通密度Bd与磁场强度Hd的比值进行定义,
用上式进行表示(参见下图)。
1-4-a. 植入磁回路磁铁的磁导系数
植入磁回路磁铁的磁导系数,可通过(6)式及(8)式求出Hd、Bd,然后将其代入(11)式求出磁导系数。
1-4-b. 磁铁单质的磁导系数
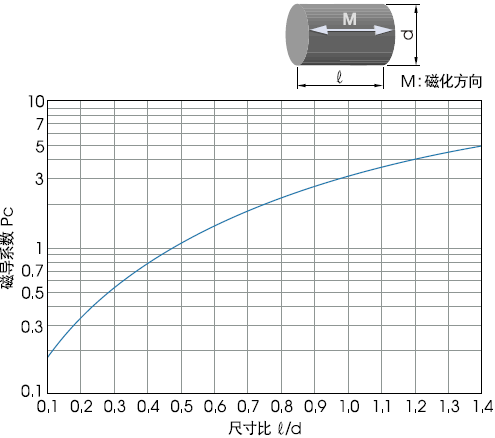
磁铁以单质形式存在时的磁导系数受到磁铁形状的很大影响,要精确地求出其值非常困难。因此,参考将圆柱形的磁铁作为测试材料的右上角图(尺寸比和磁导系数的关系图),可获得大致的目标值。
作为近似值,则为:
1-5. 长度Lm、截面积Am、体积Vm的计算方法
磁铁所需的长度Lm、截面积Am可通过
依据该计算公式,通过赋予Hd、Bd、Bg、Ag、Lg及f和σ的值,即可算出所需要的Lm、Am。 另外,必要的体积Vm为:
必要的磁铁体积与其工作点的磁能积成反比。
1-6. 漏磁系数σ、磁动势损失系数f的求解方法
1-6-a. 试验性求解σ、f时的步骤
■ 使用探测线圈的方法
- 1. 在磁铁上缠绕探测线圈,测量气隙磁通量。
- 2. 依据全磁通量Φg /磁铁截面积Am算出Bd。
- 3. 依据B-H曲线(减磁曲线)求Hd。
- 4. 实测Bg、Ag、Lg、Am、Lm。
- 5. 根据式(6)、(8),算出f、σ。
■ 不使用探测线圈的方法
- 1. 假设f值(一般为1.0〜1.2)。
- 2. 实测Lm、Bg、Lg。
- 3. 根据上页中的(12)式算出Hd。
- 4. 利用B-H曲线(减磁曲线)求得Bd。
- 5. 实测Am、Ag,利用(8)式算出σ。
1-6-b. 通过计算求解σ的方法
计算出Pg和Pf1〜Pfn,求出σ。
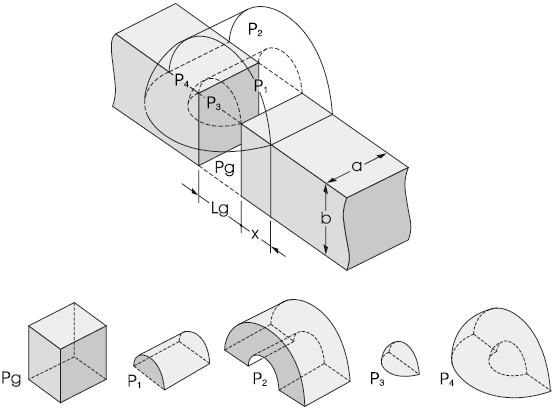
参考示例
漏磁路空间的基本构件(Pg、P1、P2、P3、P4)的磁导计算示例如下所示。
1) 图中的气隙空间部分的磁导
2) 半圆柱形的漏磁路径的磁导
3) 半圆柱形(空心)的漏磁路径的磁导空心半圆柱形的漏磁路径的磁导
4) 1/4球体状的漏磁路径的磁导
5) 空心1/4球体状的漏磁路径的磁导
通过组合上述1)〜5)种磁导,可以求得漏磁路空间中σ的概略值(μ0:真空磁导率)。
2. 磁铁中心线上的磁通密度B(X)的计算公式
当工作点Bd位于B-H曲线的直线或者压曲点上方时,可认为磁铁外部的磁场分布情况如下:假设有一个和磁铁磁导率相同的、相同断面形状、长度X的空间,可采用其外圆面上所产生的闭路电流引发的磁场相同的考虑方式。
如下所示的是三种代表性形状的B(X)求解计算公式。此类计算公式对于铁氧体磁铁及钕磁铁作为近似计算公式有效。
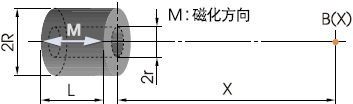
2-1. 圆柱形磁铁
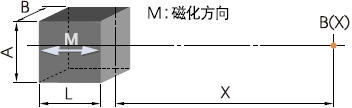
2-2. 方柱形磁铁
2-3. 圆筒形磁铁
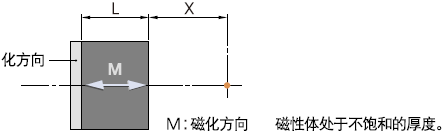
2-4. 在磁极的背面有磁性体时
在2-1、2-2、2-3式中的L项带入2L。
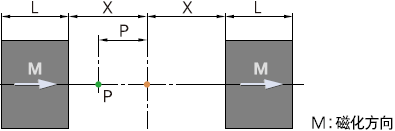
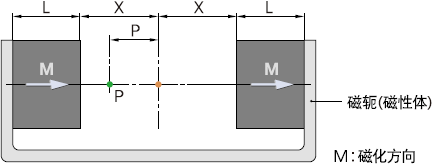
2-5. 相同形状的磁铁在2X距离相对时
在气隙中心的B(X),是采用2-1、2-2、2-3式所求B(X)的2倍。
另外,气隙中P点的B(X)为在前面计算式中X项代入X-P和X+P后的B(X-P)与B(X+P)之和。
2-6. 在与前项相同配置下,磁极背面带有磁性体时
在2-1、2-2、2-3式中的L项代入2L,气隙中心及气隙中P点的B(X)计算方式与2.5项的顺序相同。
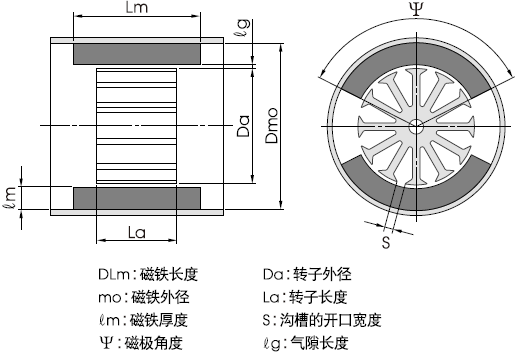
3. 电机用磁回路中有效磁通的计算
电机用磁回路因转子沟槽数、沟槽形状和壳体厚度等要素不同,磁回路条件存在很大的差异。因此,仅记述能显示该项基本思考方式的计算公式。
1) 磁铁截面积 Am
2) 磁铁等价尺寸比 ℓ/d
3) 磁铁单质的漏磁磁导系数 Pi
4) 包含磁轭部分的磁铁单质的磁导系数 PL
5) 卡特系数 Kc
6) 有效磁导系数 Pu
7) 漏磁通σ
8) 磁极磁通(或有效磁通)Φg
关于磁回路的饱和
上述Φg的计算方法未考虑磁回路的饱和状况。但对于实际磁回路来说,也考虑了壳体、转子部分所产生的饱和现象。即采用上述计算方法计算出的Φg与实际电机所产生的Φg相比,当其值小于实际电机Φg的计算值时,可以认为磁回路已处于饱和状态。
SI单位与CGS单位换算表
SI单位特性值乘以左侧标有▶ 的换算比,则为CGS单位的值。
同样,CGS单位特性值乘以左侧标有◀ 的换算比,则为SI单位的值。
| SI単位▶ | ◀CGS単位 | ||||||
|---|---|---|---|---|---|---|---|
| 磁场项目 | 项目符号 | 单位名称 | 单位符号 | 换算比▶ | ◀换算比 | 单位符号 | 单位名称 |
| 磁通 | Φ | 韦伯 | Wb | 108▶ | ◀10-8 | Mx | 麦克斯韦 |
| 磁通密度 | B | 特斯拉 | T | 104▶ | ◀10-4 | G | 高斯 |
| 磁场强度 | H | 安培/m | A/m | 4π×10 -3▶ | ◀103/4π | Oe | 奥斯特 |
| 磁化强度 | M | 安培/m | A/m | 10 -3▶ | ◀103 | G | 高斯 |
| 磁力极化 | J | 特斯拉 | T | 104/4π▶ | ◀4π×10-4 | G | 高斯 |
| 磁动势 | Fm | 安培 | A | 4π×10-1▶ | ◀10/4π | Gi | 吉伯 |
| 磁力吸引力 | F | 牛顿 | N | 105▶ | ◀10-5 | dyn | 达因 |
| 磁导率 | μ | 亨/米/m | H/m | 107/4π▶ | ◀4π×10-7 | 不名数 | |
| 真空磁导率 | μ0 | 4π×10-7亨/米/m | H/m | 不名数 | 1 | ||
| 磁阻 | Rm | 1/亨/米 | H-1 | 4π×10-9▶ | ◀109/4π | Gi/Mx | 吉伯/麦克斯韦 |
| 磁导 | P | 亨/米 | H | 109/4π▶ | ◀4π×10-9 | Mx/Gi | 麦克斯韦/吉伯 |
| 磁能积 | BH | 焦耳/m3 | J/m3 | 4π×10▶ | ◀10-1/4π | G · Oe | 高斯 · 奥斯特 |
| 10▶ | 10-1 | erg/cm3 | 尔格/cm3 | ||||